Shape Characteristics

By observing the three black shapes below one can distinguish the existence of a fourth shape implicitly created. It seems that shape is an abstract entity that exists inside the mind and does not necessarily have to be related to some material.


Shape is an abstract entity that possesses certain geometric characteristics. The implicit triangle (above) is more about a geometry of a three equally spaced points and can be recognized regardless of the variations in size, color, line weight, etc.



The study of shapes and their attributes is a part of geometry (= earth measurement). In Euclidean geometry (350 BC) there are definitions and rules that describe the behavior of the geometric entities. These entities are creations of the mind and have no correspondence to the real world. An infinite line or an infinite plane are thing that can exist only in the human mind.




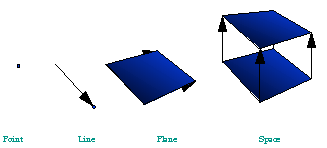
A point creating a line through its movement, a line creating a plane, and a plane creating space are abstract definitions that allows one to understand the concepts of time and space.




In Cartesian geometry (1637 AD) points are identified by their orthogonal projections (x,y,z). Shapes are defined as relationships between points, i.e. a circle is a shape where points raised to the square have a certain value (r). In other words, analytic geometry defines shapes through the relationships of points.



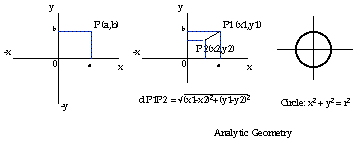
Shape definitions:
Edges are the sides of a shape. Vertices are the points where edges meet. Interior are all the points that are enclosed within the edges. Two edges are concave when the angle they meet is more than 180 degrees (else they are convex)



Irregular and regular shapes
Regular shapes are shapes that can be described through a relationship of points. Until a relationship is found that describes the location of vertices a shape is refereed to as irregular.




Shape Characteristics
A shape can be characterized and measured by the following relationships:





Area is all the points that are enclosed within the edges of a shape. The number can number of points, pixels, square feet, etc.
The perimeter is the addition of the lengths of all the edges.
Bounding rectangle is a rectangle that fully encloses the shape.
Compactness is a value that characterizes the degree of how close to circle the shape is.
Centroid is a point that is calculated by adding all the coordinates of the edges and dividing it by the number of edges (or vertices).
Eccentricity is the ratio of the circumscribed circle by the inscribed circle.

Shape Properties


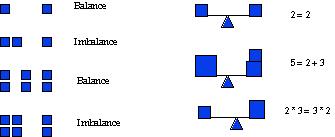
Balance
Balance is the state of distribution in which all action has come to a standstill. (Arnheim, 1977: 20)





Symmetry
Symmetry is a transformation that leaves the shape invariant




Axiality
Axiality is the arrangement of elements along a line




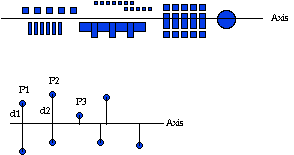
Proportion
Proportion is the quantitative comparison between things




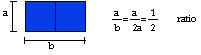
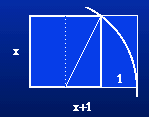
The Golden ratio




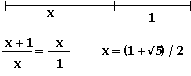
Rhythm
Rhythm is the rate of repetition









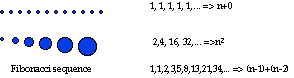
Hierarchy
Hierarchy is a scale of power, weight, or importance created visually by perceptual gradients. (Arnheim, 1982: 217)






Parti
Parti is an abstraction of a visual composition




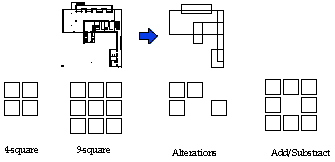
Movement and Change
Movements of shapes can be seen by the result.





Liquid Shape
Imagine a shape that constantly changes form


but maintain its four edges and vertices.
As long as it has four sides it is a valid transformation
The study of such transformations is called topology.


The mug and the key are equal "shapes" topologically because they both have one hole in them. As long as no cutting operation is performed that would destroy the identity of the hole, the two objects will be pronounced equal.


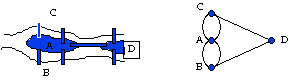
Shape Network
A shape can be represented as points and connections


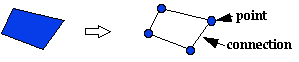
Reversely, a series of points and connections can be represented as a shape



Things to Consider:


References
Arnheim, R. The Dynamics of Architectural Form, University of California Press, 1977
Devlin, K. Mathematics: The Science of Patterns, New York: Scientific American Library, 1994
Vakalo, G.-E., Visual Studies, Nefeli, 1978.