Introduction to Computer-aided Architectural Design 3D

To mail questions or comments please click here

3D Space - Concepts of modeling

Contents

• The concept of 3D space
• Projection systems
• Object representation
• Transformation operations
• Set operations

1. The Concept of Three-dimensional Space

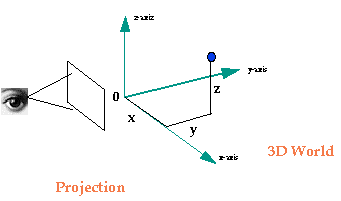
The concept of three-dimensional space is very old and very simple. By observation one can notice that the world around us is comprehensable by simply watching at it. Although there is a material existence of objects (molecules, atoms, etc.) nonetheless it is enough to use our eyes to locate objects. We do not have to physically touch objects to locate them. The eye is a piece of glass where rays from the real world are projected. Therefore we can distinguish two systems: a three-dimensional world, and a projection system. Historically, Euclid was able to specify the existence of such a world, Descartes was able to specify a system of three-directions to locate objects within such a wolrd, and others were able to develop techniques to project that world on a canvas.

2. Projection Systems

With the development of computer technology it became interesting and challenging to simulate the way humans see the world. The computer screen would be the surface of the eye, the 3-D world would be defined as x,y,z numbers in the computer's memory, and the projection calculations would be done with the computer processor. Lets take an example: a cube has eight points, and each point has three coordinates (x,y,z), therefore we need 8x3=24 numbers to describe the position of all points of the cube. Using simple mathematics we can calculate the projections of each point on the computer screen and then draw the projected cube on the screen. If we change the coordinates (move, rotate, or scale the cube) we project the points from their new position on the screen.

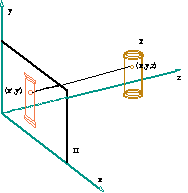
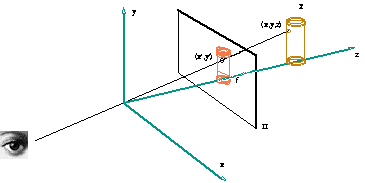
In the following figures you can see the projection of an object with parallel lines and converging lines. The first projection system is called orthographic or parallel and the second is called perspective.

3. Object Representation

Lets go back to simple geometry. An object can be composed of points and connecting lines. A square is four points and four connections. A cube is eight points and 12 connecting lines (we can also refer to the points as the geometry of the object and the connecting lines as the topology of the object). In the following example there are 10 points and 7 connecting line lists each for every face. This is essentially how an object is represented internally as lists of numbers in the computer's memory. In addition to this information one can add attributes such as color, material, etc.

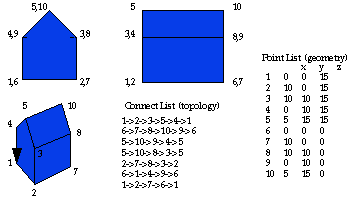
Three-dimensional objects can be created in many different ways:

• Extrusion. Here a 2D shape is extruded into a 3D object either by parallel lines of extrusion (such as a circle into a cylinder) or the extruded lines meet at a point (such as a circle into a cone)
• Revolution. Here a 2D shape is revolved around an axis creating a 3D object of revolution (such as a hemicircle into a sphere)
• Result of set operations. Here an object is the result of union, intersection, and difference operations of elementary objects (such as cubes, spheres, cylinders, cones, etc.). We call these elementary objects primitives. Set operations will be discussed later in these notes.
• Clouds of points and meshes. Here an object is represented as a set of points. When these points represent a surface in space and are connected as a grid we call it a mesh.

4. Transformation Operations

As mentioned earlier, three-dimensional objects are stored in the computer's memory as numbers representing points and connections. Then these points are projected to the surface of the screen. Any change in the geometry (that is, the location of the points) is called a transformation. In the figure below each point of the object was multiplied by a series of sines and cosines resulting in creating the impressionof rotation.

We distinguish many transformations, but the most important are:

Translation

Translation is another word for moving and object to a new position. It also sometimes called offsetting. Basically, it is the change of location of the object in space. By adding a constant number (i.e. 5 units) to the x coordinate of all points the object is moved in the x direction (by 5 units).

Rotation

A rotation specifies a pivoting, or angular displacement about an axis. Objects are rotated by specifying an angle of rotation and a pivot point. Then trigonometric functions are used to determine the new position.

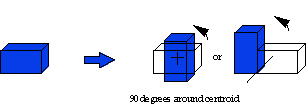
Scale

Scale (or sizing) either reduces or enlarges an object. Objects are scaled by specifying a percentage of scaling, the direction, and a pivot point. Then simple multiplication of each coordinate determines the new position.

5. Set Operations

Set operations are logical combinations of objects. They behave as if the objects have mass. Imagine two object that are composed of molecules. The AND operator defines a new object that combines all the molecules of object A AND object B. To be more specific:

Union

For two objects A and B the union operator defines a new object that combines all the molecules of object A AND object B.

Intersection

For two objects A and B the intersection operator defines a new object that combines all the molecules that are common to object A and B.

Difference

• Case 1 (A-B): For two objects A and B the difference (A-B) operator defines a new object that combines all the molecules that are in object A minus those in object B.
• Case 1 (B-A): For two objects A and B the difference (B-A) operator defines a new object that combines all the molecules that are in object B minus those in object A.

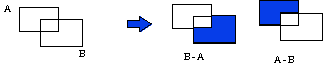
References

• Friedhoff, R., "Visualization", New York: Freeman and Co., 1989.
• Kerlow, I. and Rosebush, J., "Computer Graphics", New York: Van Nostrand Reinhold, 1994.
• Mitchell, W., "Computer-Aided Architectural Design", New York: Van Nostrand Reinhold, 1977.