15.
Simple
Trigonometry
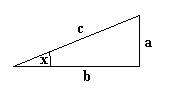
Trigonometry is the study of the relationships among the angles and sides of a triangle. Sine of angle x is the ratio of a/c and cosine is the ratio b/c in the triangle below:
Now the interesting thing about sines and cosines is that when we calculate their value for smoothly changing angles we get a “circular” behavior. Consider the following code example:
import java.applet.*;
import java.awt.*;
public class simple extends Applet{
//*****************************************
public void paint(Graphics g){
for(int i=0; i<500; i++){
int x = i;
int y =
(int)(50. * Math.cos(Math.PI/180.* i)
);
g.drawString(".", x , y+100);
System.out.println("x = " + x + " y =
" + y);
}
}
}
Reminder: 180 degrees is equal to PI radians. So to convert x degrees to r radians, we do x = PI/180*r radians. Since Math.sin and Math.cos take for angles radians we always need to convert degrees (0-360) to radians (0.0 – 3.14159).
In the code above, we loop to 500 and for x we pass the counter i (so we have a linear progress of one pixel in x) and for y we get the cosine of the counter i (converted to radians), then exaggerated by 50.0. Since the result is a double we cast it to int to assign it to y.
int x = i;
int y = (int)(50. *
Math.cos(Math.PI/180.* i) );
Then we draw the result using a drawstring with a “.” (period) as the String. So, again, x moves on a linear fashion (0, 1,2,3,4,5,…,499) and y move in the y-direction up and down (we also move it 100 pixels lower to be in the center of the screen) in the following way:
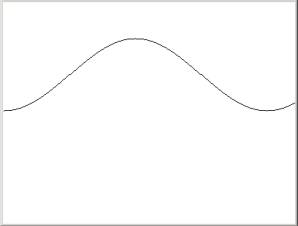
So the result is a set of dots (“.”) starting as at (0,100) and then as x goes from 0,1,2,3,4…500, y produces cosines (that we know from mathematics that will always be between 0. and 1.) that we multiply by 50. to make y go between 0. and 50.
So if we want to shorten the curve we need to do the following adjustments:
for(int i=0; i<5000; i++){
int x = i/10;
int
y = (int)(50. * Math.cos(Math.PI/180.*
i) );
g.drawString(".", x , y+100);
System.out.println("x = " + x + " y = " + y);
}
We know that a curve will do a full circle when i is 360 so in 5000 it will 5000/360 = 13.8 full circles but we don’t want x to go to 5000 because the screen is only 400 pixels long and it will run out of sight. So we divide i by 10 and therefore I will go to 500 only.
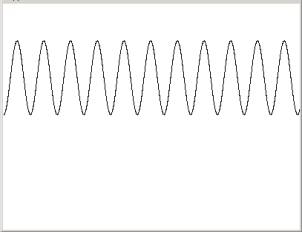
If we reverse the order of x and y that is:
for(int i=0; i<5000; i++){
int
x = (int)(50. * Math.cos(Math.PI/180.*
i) );
int y = i/10;
g.drawString(".", x+100 , y);
//System.out.println("x = " + x + " y = " + y);
}
we will get the predictable result:
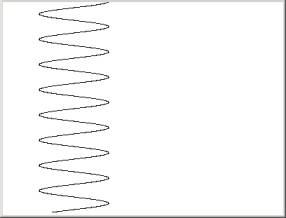
because y is linear and x is “trigonometric”.
Now if we combine the two together alternating sine and cosine in the following code:
for(int i=0; i<5000; i++){
int x = (int)(50. * Math.cos(Math.PI/180.*
i) );
int y = (int)(50. * Math.sin(Math.PI/180.*
i) );
g.drawString(".", x+100 , y+100);
//System.out.println("x = " + x + " y = " + y);
}
we will see the following unexpected result:
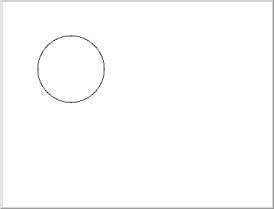
A circle! This trick we will use later on to rotate objects in the screen, because basically what we are doing here is forcing x and y to move on the periphery of a circle. We actually forced x and y to rotate around a center 13.8 times (since the counter goes 0-5000). If the counter was going from 0-180 as shown below:
for(int i=0; i<180; i++){
int x = (int)(50. *
Math.cos(Math.PI/180.* i) );
int y = (int)(50. *
Math.sin(Math.PI/180.* i) );
g.drawString(".", x+100 , y+100);
}
we would have gotten a half-circle (because i is the degrees of the rotation)
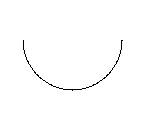
16.
Polygons
A polygon as defined in the Graphics class through the method g.drawPolygon is an object that has n points. We create a new polygon object (empty initially) through the statement:
Polygon p = new Polygon();
The name of the polygon is p, it is of type Polygon and we use new to allocate memory since it is of a more-than-one size. The polygon() is one of the ways to create a new polygon (the object Polygon can be found in the Café’s menu Help->Java API Reference->Index).
Then we add points to the polygon. For example, the following code creates a triangle.
p.addPoint (100,100);
p.addPoint (150,200);
p.addPoint (50,200);
The p. means that we are adding to the object p. In other words we are using the Polygon’s method addPoint(int x, int y).
Finally, we draw or fill the polygon through the statements:
g.drawPolygon (p); or
g.fillPolygon (p);
The following code shows how to create a simple triangle by inserting the actual numbers of the x and y locations (this is called hardcoding because we not using variables):
import java.applet.*;
import java.awt.*;
public class simple extends Applet{
//*****************************************
public void paint(Graphics g){
Polygon p = new Polygon();
p.addPoint (100,100);
p.addPoint (150,200);
p.addPoint (50,200);
g.fillPolygon (p);
}
}
The result is a predictable triangle:

Polygons are very important in 2D graphics (3D too) because they allow us to create any shape.
16.1.
Polygons through arrays
Another way to create a polygon is through an array of x and y coordinates according to the syntax:
Polygon
p = new Polygon(xArray, yArray, n);
Now, if n = 3 we need to create the arrays with four integers. That is:
int n= 3;
int[] xArray = new int[n];
int[] yArray = new int[n];
Then we need to fill the arrays with integers to draw the polygon. Here is the code:
import java.applet.*;
import java.awt.*;
public class simple extends Applet{
//*****************************************
public void paint(Graphics g){
int n = 3;
int[] xArray = new int[n];
int[] yArray = new int[n];
xArray[0] = 100;
yArray[0] = 100;
xArray[1] = 150;
yArray[1] = 200;
xArray[2] = 50;
yArray[2] = 200;
Polygon p = new Polygon(xArray, yArray, n);
g.drawPolygon (p);
}
}
In this example we used the arrays to fill-in the points and then we pass them to the polygon. This method is a little better because through the arrays we can control what is written to the arrays. Specifically, it would be great if we could create an algorithm that would fill the arrays instead of hardcoding the data (as we did with the previous example in section 16).
16.2.
Circular polygons
In section 15 we saw how to rotate points in a circle and in section 16.1 we saw how to create polygons through arrays of points. Now the logical deduction is that we should be able to connect the two sections and create circular polygons, that is, polygons created through arrays that are filled by rotating points on a circle. In the following code we demonstrate this algorithm:
import java.applet.*;
import java.awt.*;
public class simple extends Applet{
//*****************************************
public void paint(Graphics g){
int n = 5;
int[] xArray = new int[n];
int[] yArray = new int[n];
double angle = 2 * Math.PI / n;
//divide the full
//circle in n
sections
for(int i =0; i< n; i++){
xArray[i] = (int)(100. + 50. * Math.sin(angle*i));
yArray[i] = (int)(100. + 50. * Math.cos(angle*i));
}
Polygon p = new Polygon(xArray, yArray, n);
g.drawPolygon (p);
}
}
After we create the arrays of n size we need to fill them with points. So we need to loop for n times and each time we have to assign the x and y values. These values are calculate through the following algorithm:
First, we divide a full circle (2*PI) by the n, the number of sides (or the size of the array).
Then, within the loop we calculate the sines and cosines by multiplying the counter (0,1,2,3,4) times the division. So if divided the circle in five pieces, every time we multiply the by the counter we get 0,1,2,3,4 times the divisions producing the five coordinates needed to draw a pentagon.
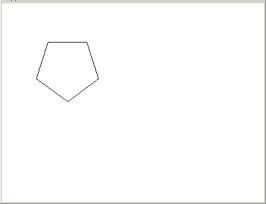
One last note: if we want to organize the code in a better way, we can create a method called makeNormalPolygon and all we need to pass is a the number of sides. This code would look like this:
import java.applet.*;
import java.awt.*;
public class simple extends Applet{
//*****************************************
public void paint(Graphics g){
Polygon p = makeNormalPolygon(5);
g.drawPolygon (p);
}
//*****************************************
public Polygon makeNormalPolygon(int nsides){
int[] xArray = new int[nsides];
int[] yArray = new int[nsides];
//divide the full circle in nsides sections
double angle = 2 * Math.PI / nsides;
for(int i =0; i<nsides; i++){
xArray[i] = (int)(100. + 50. * Math.sin(angle*i));
yArray[i] = (int)(100. + 50. * Math.cos(angle*i));
}
Polygon p = new Polygon(xArray, yArray, nsides);
return p;
}
}
So makeNormalPolygon is a method that takes an integer number, which indicates the number of sides and returns a Polygon that is then used by paint to draw it on the screen (it also public so other classes can call it).